Penn en Teller, de magie van het onmogelijke
Het probleem dat ik u voorgeschoteld heb heeft bij velen tot hoofdbrekens geleid. In de opgave staat dat wit naar beste vermogen speelt maar dat zwart er desondanks in slaagt remise te maken. Dat ziet er op het eerste gezicht onmogelijk uit. Op de clubavond kreeg ik reacties als: ‘ik heb me suf gepiekerd maar kom er niet uit’, ‘het diagram zal wel niet kloppen’, ‘ik snap er helemaal niets van’, ‘wit zal dan wel niet mat geven en iets anders doen’, ‘het is vast een tikfout’ en dergelijke.
Het diagram en de opdracht zijn wel degelijk juist en dat zou moeten uitdagen verder te denken. Hoe kan iets dat op het eerste gezicht onmogelijk lijkt toch gerealiseerd worden? Dat is de vraag die goochelaars zich stellen. De uitdaging is de creatieve hersencellen aan het werk te zetten, dat geldt ook voor de opgave. Daarom gaf ik aan dat een oplossing niet ‘goed’ hoefde te zijn. Een creatieve of amusante poging, hoe gedetailleerder hoe beter, op zich is al genoeg.
Om u daarbij enigszins op weg te helpen heb ik geschreven dat ik een hint heb gegeven, zonder aan te geven welke.
Denksystemen
Interessant is dat de gegeven reacties op de opgave typische Systeem 1 reacties zijn. Om dat uit te leggen een stukje theorie.
Ons brein is ingesteld op het vinden van ‘makkelijke’ oplossingen, het is lui. Dat is in het dagelijks leven prima zodat we snel beslissingen kunnen nemen in complexe situaties. Daniel Kahneman legt in zijn boek ‘Ons Feilbare Denken’ (‘Thinking Fast and Slow’) uit dat we over twee denksystemen beschikken. Hij noemt die gemakshalve Systeem 1 en Systeem 2 (wat ik dan weer typisch Systeem 1 vind).
Systeem 1 is ons intuïtieve denken. Het automatische en snelle denken op basis van indrukken, ingevingen, intenties en gevoelens waar we nauwelijks of geen moeite voor doen. Het denken dat te pas komt wanneer u:
* Een antwoord geeft op de vraag ‘Wat is de hoofdstad van Frankrijk?’;
* Een makkelijke som oplost (1 + 1 = …);
* Een auto bestuurt op een lege weg.
Het gebruik van Systeem 1 kost weinig inspanning en wordt gebruikt om dagelijkse probleempjes op te lossen.
Systeem 2 is ons weloverwogen denken. Het is het trage denken dat energie opslorpt. Het denken dat te pas komt wanneer u:
* Uw aandacht richt op een gesprek in een lawaaierige ruimte;
* In uw geheugen graaft naar iemands naam;
* Telt hoe vaak de letter E in deze zin voorkomt.
De twee systemen zijn tegelijk actief. Systeem 1 heeft standaard de leiding, terwijl Systeem 2 in een sluimerstand werkt. Systeem 1 genereert voortdurend suggesties die doorgaans klakkeloos worden overgenomen door Systeem 2. Bijvoorbeeld dat 1 + 1 gelijk is aan 2. Allesbehalve een breinkraker. Raakt Systeem 1 in de problemen omdat het niet met 1 + 1 maar met 18 x 37 te maken krijgt? Dan schiet Systeem 2 wakker en komt het Systeem 1 te hulp.
Duidelijk is dat te veel vertrouwen op Systeem 1 kan leiden tot fouten en te snel genoegen nemen met een ‘oplossing’ als: ‘dit kan niet’.
Voor het oplossen van de opgave, en creatief denken, is het inschakelen van Systeem 2 dus noodzakelijk.
Creatief oplossen
Schaken is een creatief spel.
Ik ben ervan overtuigd dat puzzels oplossen waarbij er ‘om het hoekje’ moet worden gedacht ons creatieve schaakbrein helpt ontwikkelen. ‘Om het hoekje’ denken, Edward deBono noemde dat zo’n 50 jaar geleden ‘lateraal denken’, oftewel bewust op een andere manier dan gewoonlijk kijken naar feiten. Een term die nu gebruikt wordt is ‘Omdenken’, Berthold Gunster is auteur van een aantal interessante en vermakelijke boeken. Voorbeelden die Gunster geeft: als het waait bouwen sommigen mensen windschermen, anderen bouwen windmolens. Wat doen we als het regent? Kinderen spelen in de plassen, volwassenen zetten paraplu op.
Of het verhaal van de wandelaar die bij een rivier komt maar geen brug of doorwaadbare plaats ziet. Hij roept naar een boer die aan de overzijde van de rivier loopt of hij weet hoe hij, de wandelaar, aan de andere kant kan komen. Waarop de boer antwoordt: ‘Daar ben je toch al?’
Het hangt er maar vanaf van welke kant je het bekijkt. Creatief denken is ook de boel omkeren.
Het oplossen van het Penn en Teller-probleem kan alleen door op een manier naar het probleem te kijken die een stap verder gaat dan ‘dit kan niet, wit zet mat en kan het dus geen remise zijn’. Door het idee te hebben dat het niet kan legt de oplosser zich een beperking op die er, gezien de opdracht ‘zwart maakt remise’ niet kan zijn.
Hoe we ons beperkingen opleggen en wat dat betekent voor het bedenken van oplossingen kan geïllustreerd worden met deze bekende puzzel:

De opdracht: Hoe kun je, zonder je potlood van een vel papier te halen, alle negen punten met elkaar verbinden door middel van vier rechte lijnen? Geen dikke pen gebruiken. De lijnen moeten door het middelpunt van de punten gaan.
Nog een verhelderend voorbeeld: Een geit zit vast aan een touw van 2 meter. Zes meter verderop ligt een baal hooi. Toch kan de geit zonder problemen van het hooi eten. Hoe kan dat?
Hint voor beide vraagstukken: kijk verder dan de neus lang is. Oplossingen aan het eind van dit artikel.
Het voorbeeld van de negen punten gaf ik ook in mijn scriptie ‘Mentale Training voor schakers’ (oktober 1980) voor de opleiding tot Schaakinstructeur B. Het oplossen van ongebruikelijke problemen stimuleert het creatieve schaakdenken. Creatieve oplossing bedenken kan door het oplossen van problemen uit het zogenaamde Fairy Chess, maar dan wel met de gebruikelijke stukken. Uit de scriptie nog twee opgaven.
Voorbeeld 1
Wit geeft mat in 4 zetten. De beperking is dat gedekte stukken niet mogen zetten.
Uit: T.R. Dawson: Caïssa’s Fairy Tales
Voorbeeld 2
Wit geeft mat in 2 zetten
Uit: 64 (Russisch schaak- en dam weekblad), 1 april 1970
Oplossingen van de schaakproblemen
Voorbeeld 1
Dit wijst zich vanzelf:
1. c2-c4, Ka1-a2; 2. Kd4-c5, Ka2-a3; 3. Kc5-b5, Ka3-a2; 4. Tb7-a7 mat.
Voorbeeld 2
Ziet er onmogelijk uit. Als de dame naar d7 kan is het mat, maar nu staat de zwarte koning pat. Zwart zou dus nog een zet moeten kunnen spelen. Hoe is dat op te lossen?
Als je je realiseert dat het in een 1-aprilnummer staat moet er iets gaan dagen… Hoe kunnen die twee vliegen in één klap geslagen worden?
1. e7-e8 promoveert tot zwarte koning!!; Ke8-d8; 2. Dg7-d7 en beide koningen staan mat!
De oplossing van het Penn en Teller probleem
Een lange inleiding om eindelijk naar de oplossing van het ‘onoplosbare’ probleem te gaan. Maar hopelijk heeft het ergens in het achterhoofd nog wat ideeën opgeleverd.
De vraagstelling ‘wit speelt, zwart maakt remise’ is gebaseerd op een werkelijk gespeelde partij. Het diagram bij de opgave komt niet uit de partij maar geeft wel de essentie weer. Want om mensen met een uitgebreide en recente database (de partij is uit 2018) op een dwaalspoor te brengen heb ik de stukken opgeschoven. In de partij staan de stukken ten opzichte van het gegeven diagram twee rijen naar rechts en de loper niet naast de koning.
Het juiste diagram is
en is uit een partij tussen Maxime Lagarde en N. Krishna Teja, Sitges 2018.
In de opgave staat dat wit naar beste vermogen speelt. Wit doet in de partij uiteraard 121. Tc8+ met mat. Nou ja, bijna mat, want zwart heeft nog één zet om te pareren en speelt 121. …, Td8. En claimt remise.
Hoe dat kan, immers na 122. Txd8 is het mat? Dat is de beperking die we onszelf opleggen en ons verhindert verder door te denken.
Het antwoord dat ik zocht is verwijzing naar artikel 9.3 van de ‘FIDE-regels voor het schaakspel’. Met deze zet claimt zwart remise omdat hij kan aantonen dat ‘… de situatie wordt bereikt, dat er met de laatste 50 opeenvolgende zetten van beide spelers geen pion is verzet en niets is geslagen.’
Het juiste antwoord was dus remise op grond van de 50-zettenregel.
Wat was de hint?
De hint is (dat kwam mooi uit!) verstopt in de namen van de goochelaars: Teller, want je moet wel goed tellen wanneer de 50 zetten zijn gedaan.
Voor de volledigheid het slot van de partij:
De winnaar
Er is, helaas, door slechts één van de leden een oplossing ingezonden. Kees Kerkdijk zette zijn creatieve hersencellen aan het werk en bedacht deze oplossing:
Wit speelt Ta8 schaak. Zwart, goochelaar zijnde, beweegt zijn rechterhand vooruit richting b-lijn en tovert (uit zijn mouw) in het voorbijgaan van veld b8 daarop een dame. Dus zet van zwart Db8 schaak.
Er zit voor wit (duidelijk geen goochelaar) niets anders op dan Tb8x en na Tb4xb8 is een remisestelling ontstaan.
Een creatieve oplossing die gebruik maakt van het gegeven dat het gaat om goochelaars. Dat was niet de hint die ik bedoelde, maar in de opgave gaf ik aan dat het erom ging een oplossing te bedenken, het hoefde niet de oplossing van de 50-zettenregel te zijn. Een creatieve af amusante oplossing was ook prima.
Toen ik Kees liet weten dat er een oplossing is die binnen het schaken blijft kwam hij met de 50-zettenregel.
Kees wint de prijs en krijgt bovendien een eervolle vermelding voor zijn creatieve vondst!
Oplossing negen punten
Veel mensen zien niet hoe het probleem op te lossen is. Ze blijven het proberen en kunnen wel alle punten met elkaar verbinden, maar het lukt niet met vier lijnen. De beperking is dat de meeste mensen de negen punten als een vierkant zien en men er onbewust vanuit gaat dat de oplossing binnen het vierkant gevonden moet worden. Als we die beperking los laten en buiten het kader denken kan is de oplossing niet moeilijk meer:
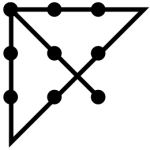
De lijnen gaan buiten het veronderstelde kader, de negen punten die als een vierkant zien. De oplossing voor het Penn en Teller probleem is eveneens te vinden door buiten het kader te denken.
Ten slotte
Het antwoord op de vraag over de geit. Ook hier moeten we los zien te komen van een beperking die we onszelf opleggen. De geit loopt namelijk gewoon naar de baal hooi toe. Er staat nergens dat het touw behalve aan de geit nog ergens anders aan vast zit.


















